要以張量方式設計多層的全連接層神經網路，須分別定義各層的權重矩陣W和偏移值向量b。有多少個全連接層，需定義數量相對的W和b，且每層權值矩陣與偏移值只能在當層使用。
假設一個全連接層神經網路，輸入:[b,784]，隱藏層有三層，輸出:[10]，在想像這這畫面時如下圖: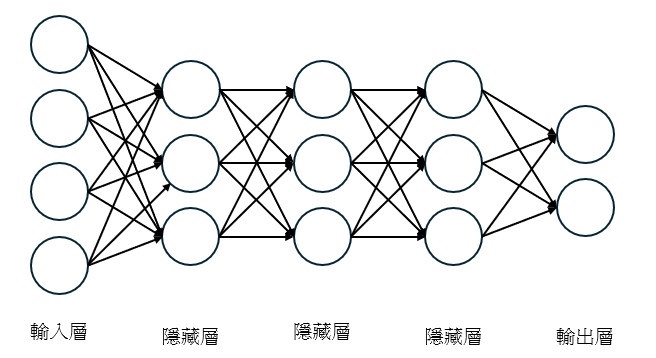

# 創建 W, b 變量
x = tf.random.normal([3, 784])

# 隱藏層 1 權重與偏置值設定
w1 = tf.Variable(tf.random.truncated_normal([784, 256], stddev=0.1))
b1 = tf.Variable(tf.zeros([256]))

# 隱藏層 2 權重與偏置值設定
w2 = tf.Variable(tf.random.truncated_normal([256, 128], stddev=0.1))
b2 = tf.Variable(tf.zeros([128]))

# 隱藏層 3 權重與偏置值設定
w3 = tf.Variable(tf.random.truncated_normal([128, 64], stddev=0.1))
b3 = tf.Variable(tf.zeros([64]))

# 輸出層權重與偏置值設定
w4 = tf.Variable(tf.random.truncated_normal([64, 10], stddev=0.1))
b4 = tf.Variable(tf.zeros([10]))

# 前向計算
o1 = x@w1 + b1
s1 = tf.nn.sigmoid(o1)

o2 = s1@w2 + b2
s2 = tf.nn.sigmoid(o2)

o3 = s2@w3 + b3
s3 = tf.nn.sigmoid(o3)

o4 = s3@w4 + b4

print(o4.shape)

輸出(3, 10)